力学家介绍（二）_行业新闻_苏州亚诺天下仪器有限公司-官网

二、伽利略对静力学所做的贡献

   伽利略在静力学上ZUI重要的贡献是给出了ZUI早一般表达的虚速度或虚位移原理。他指出：一个质点系在给定力系的作用下所得到的各点速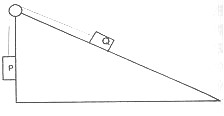度或位移分量与质点系内部连接条件是相容的。当质点系通过一个平衡位置时，各个力同他们各自作用的质点分速度的乘积的总和等于零（后半句是19世纪法国力学家科里奥利（Coriolis）的表述）。伽利略利用这条原理处理过滑轮组与斜面问题。他处理滑轮与斜面问题的方法是这样的。如图所示，若下落，升高，则。
   伽利略得到的方程是这里是的位移  是的位移。
   伽利略在阿基米德之后重新作实验证实流体静力学的浮力定律。他把虚位移原理与流体平衡联系起来，这种观点后来为帕斯卡所充分发展。

   三、伽利略关于固定端悬臂梁的承载力研究
   伽利略在他《关于两种新科学的对话》（1638年）提到、考察了固定端悬臂梁的承载能力的问题。
   令为梁长，为高，为荷载，为梁根部的纵向反力，为横向反力，为梁根部的弯矩，为抗力矩，他得到的结论是，  。伽利略给出了8个命题，分别讨论各量之间的关系，其中有些重要的结论列举如下：
   “长度与厚度都相等的棱柱体和圆柱体具有的抗断裂力（即臂端承载能力）与截面的直径立方成正比，而与长度成反比。”即
，
   伽利略接下来讨论了等强度梁的截面问题以及在自重下梁的强度问题。
   关于两端支承而中间受载梁，伽利略认为中间是危险点，，从而靠支承点的材料可以削去。
   此外，他还讨论了空心圆截面梁（管梁）。

胡克的生平与胡克定律

英国力学家胡克（Robert Hooke，1635-1703）其父是怀特岛（High，在英吉利海峡内）上的一位牧师。他13岁入小学，住在校长的家中，在那几年内学会了拉丁文、希腊文和希伯来文，学通了欧几里得几何和一些数学课题。1653年，胡克被派到牛津的基督教堂当唱歌队的指挥员，在这个位置上，他坚持自学，于1662年得到工艺学硕士学位。在牛津他得以接触一些有名的科学家，而他当时的工艺很熟练，所以他曾帮那些科学家做过实验。特别他帮助当时的大科学家波义耳（Robert Boyle ，1627－1691）做研究工作，由于他的巧手才使波义耳的空气泵取得成功。

1663年胡克成为英国皇家学会的会员，并且从1677年到1683年当秘书，从1662年一直到死，都是该会的实验总监。

胡克有多方面的才能，他不仅在力学方面有贡献，他在化学、物理学、天文学、生物学等方面都有重要的贡献。他写过一本《显微术》的书，书中记载了他对显微镜的改进，也记载了他利用显微镜的发现。此外他还是一位积极钻研和传播武术的教师。在科学研究上他是一位十分灵巧而能干的实验大师，他在理论上的工作方面也很多，但是多数是不够严密和完整的。

胡克的性格乖僻，喜欢同别人争论，而常常声称某某发明是他先于别人有想法。

胡克在力学上ZUI为出名的工作是首先研究了弹簧，得到了外力与变形成比例的结论，后人也称之为胡克定律。

1678年胡克发表了题为《弹簧》的论文，它包含了胡克对于弹性体的实验结果。文章在描述他的实验时说：“取一根长20、或30、或40英尺的金属丝，把上端同钉子系牢，而下端系一弹簧秤以承受砝码。用两脚规量出自秤盘底至地面的距离，把这一距离记下来。再将若干砝码加到秤盘上，并顺序记下金属丝的伸长量。ZUI后比较这些伸长量便可以看到砝码与砝码引起的伸长量彼此之间存在着同样的比例。”

胡克一共用四种弹性物体来进行他的实验。除了金属丝之外还有：

一个轴铅垂的金属螺旋线，上端固定下端系秤盘和砝码，随着载荷增加螺旋成正比例地伸长。

把一根钟表发条上紧成垂直的螺旋，内端固定，外端附着在一个与此发条同轴的轻巧的齿轮的轮毂上，后者盘绕着一根丝线，丝线的自由端悬吊一个很轻的秤盘，秤盘中加多大的硅码，这齿轮便旋转相应的角度。

给干燥木质的悬臂梁的自由端加上载荷，挠曲变形也符合这条定律。

早在1665年，他在《显微术》一书中便指出过，这条定律同样适用于压缩空气。他并且利用这一理论建议制造弹簧秤。

英国科学家波义耳在1662年与马略特在1676年二人各自独立地建立了气体压强与体积关系的定律。它也可以看为与胡克同一时代同一类型的定律，胡克定律是对固体的，波义耳是对气体的。

牛顿的生平

牛顿（Isac Newton，1642－1727）出生于林肯郡伍尔索朴城的一个中等农户家中。在他出生之前父亲即去世，他不到三岁时母亲改嫁了，他不得不靠他的外祖母养大。从小的这种境遇使他的性格有点怪，对人尖刻而又多疑。他在12岁的时候入当地一所普通中学读书。他学习拔尖，在课余能做些机械玩具与机械模型。他曾为当地造过一只水钟，一直到他离开那里时还在使用，他在这段时间制做的日晷直到现在还保存着。

牛顿的母亲二次结婚后继父又去世了。于是牛顿失学回家帮助管理农庄。然而他对这些事没有兴趣，就又回到学校，后来进人剑桥大学。

1661年牛顿进入了剑桥大学的三一学院，1665年获文学学士学位。在大学期间他全面掌握了当时的数学和光学。1665－1666的两年期间，剑桥流行黑热病，学校暂时停办，他躲避瘟疫回到老家。这段时间中他发现了二项式定律，据他自己说还想到了流数法即后来的微分学，开始了光学中的颜色实验，即白光由7种色光构成的实验，而且由于一次躺在树下看到苹果落地开始思索地心引力问题。1669年，他的老师和亲密的朋友巴罗（Isaac Barrow，1630－167 7）辞去卢卡辛数学讲座，26岁的牛顿受聘继任了这个职位。在30岁时，牛顿被选为皇家学会的会员，这是当时英国的ZUI高科学荣誉。

牛顿在光学上的主要贡献是发现了太阳光是由7种不同颜色的光合成的，他提出了光的微粒说。他的微粒说与惠更斯的波动说，形成光的本质问题的争论，一直延续了数百年。牛顿发明了反射式望远镜。

牛顿在数学上的主要贡献是与莱布尼兹各自独立地发明了微积分，给出了二项式定理。

牛顿在力学上ZUI重要的贡献，也是牛顿对整个自然科学的ZUI重要的贡献是他的巨著《自然哲学的数学原理》（简称〈原理〉）。这本书出版于1687年，书中提出了万有引力理论并且系统总结了前人对动力学的研究成果，后人将这本书所总结的经典力学系统称为牛顿力学。

在科学史上牛顿是一个迷恋学术、不拘小节的典型。有的传记作家描写他是：“从不作任何娱乐和消遣，他不骑马外出换换空气，不散步，不玩球，也不作其他任何运动，认为不花在研究上的时间都是损失。”他常常工作到后半夜，往往忘记吃饭，生活上也不修边幅。当他沉缅于学术问题时，甚至糊涂到嘱咐仆人给同一个窝里的一大一小的两只猫各开一个洞。

由于牛顿的脾气乖僻，不善于同人相处，牛顿终生未娶。

牛顿出生于基督教的家庭，他是一位虔诚的教徒，在完成了《原理》之后，便一直从事《圣经》的研究，有关这方面的著作手稿有150万字之多，绝大部分没有出版。

牛顿还卷人了一场与莱布尼兹关于微积分的发明权的论争，牛顿竟然默许莱布尼兹是剽窃者，说明他对自己的发现有强烈独占的情绪。事实上，微积分ZUI早的论文是莱布尼兹 1684年发表的，比牛顿的《原理》早了3年。

50岁以后，牛顿对学术问题就不太感兴趣了，而把兴趣放在多赚钱上。有人推荐他去担任伦敦的一所贵族的上流学校的校长，牛顿以“每年不过是200镑，还得每天关在伦敦不出去。”为理由谢绝了。他于1696年，先被任命为造币局的知事，后又成为经理，之后他就真心实意地去赚钱了。除了赚钱之外，牛顿的晚年还对炼金术和神学感兴趣。

牛顿力学系统与万有引力的证实

牛顿的《原理》一书出版后，有一系列的事实证实了这一理论的正确性。我们选其重要者介绍如下：

哈雷彗星 1705 年哈雷（Edmond Hally，1656－1742）在《彗星天文学》书中，以万有引力定律为基础，推算了历史上24颗彗星的轨道。当他计算1682年的彗星轨道时注意到与开普勒1607年观测到的彗星轨道很接近，后来又找到1531年的彗星轨道也差不多，而且这三颗彗星的轨道都为75—76年，于是他断言这三颗彗星是同一颗。在书中他预言这颗彗星将于1758年再度回归。1758年，在哈雷已去世了16年时，这颗彗星准时回归，它证明了根据万有引力理论计算结果预言的正确性。这颗彗星后来以哈雷命名。

海王星的发现 1781年3月，威廉·赫歇尔（Frederick william Herschel，1738-1822）发现了天王星之后，人们还发现，早在16世纪在天文观测资料里就有它的记录，不过当时把它当作一颗恒星罢了。后来一直记录它的位置，到了1821年连同1871年以前，已经积累了130年的观测资料。法国天文学家布瓦尔（Alexis Bouvard，1767—1843）在星历表上发现木、土二行星的计算与观测符合得好，而天王星不好，1781年前的观测与1781年后的观测记录不在一个椭圆上。布瓦尔便去掉了1781年以前的观测资料重新编制星表。到了1830年，英国的天文学家又发现布瓦尔的星表与新的观测数据又产生了大约的误差，并且有增无减。英国天文学家们又对他们数十年来的观测资料进行复核，结果还是别的行星符合很好，就是天王星不好。这时，有人提出疑问，猜想在天王星之外还有一颗行星。但要反推这颗行星的位置却十分困难。1845年一位英国青年天文学家与1846年一位法国青年天文学家先后根据万有引力理论算出这颗新星的轨道，终于在1846年9月由柏林天文台的伽勒（Johann Gottfried Galle，1812—1910）在预期的位置上发现它，并命名为海王星。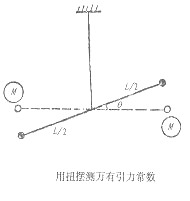

万有引力常数 在牛顿的《原理》中，万有引力定律的表述还不够简练。后来人们把它写为：引力，其中与为互相吸引的两物体的质量，为它们之间的距离，为万有引力常数。的值直到1798年才由英国学者卡文迪什（Henry Cavendish，1731—1810）利用扭秤测得。卡文迪什将一根均匀两端带有质量球的秤杆中点用细金属丝悬挂，再以两个质量为的球置于各与为适当的距离，且与秤杆垂直处。这时测量秤杆的偏角，求出金属丝承受的扭矩，便可以得到引力，进而可以得到。目前，根据1976年国际天文学联合会天文常数系统的常数表，万有引力常数值为＝。

铁摩辛柯与他的著作

在力学教育中，我们应当特别介绍一下铁摩辛柯（Stephen P．Timoshenko，1878－1971）他出生于乌克兰，去世于德国，190l年毕业于俄国彼得堡交通道路学院。之后他按规定服役一年，于1902年回彼得堡交通道路学院任实验讲师，一年后到彼得堡工学院任讲师。从 1903年到1906年，他每年利用夏天的时间去德国哥廷根大学进修，在克莱因、普朗特的指导下进行研究工作。在1907－1921年间先后在基辅、彼得堡与南斯拉夫任教。

从1922年铁摩辛柯到美国费城振动专业公司，第二年到匹兹堡威斯汀豪斯电器公司从事力学研究工作。从1928年起他在美国密歇根大学、1936年到斯坦福大学任教。

在力学研究方面，铁摩辛柯ZUI杰出的工作是在梁的振动问题中计入了旋转惯性与剪力，这种模型后来被称为“铁摩辛柯梁”。此外他在圆孔附近的应力集中、梁板的弯曲振动问题、薄壁杆件扭转问题、弹性系统的稳定性问题上都有重要的工作。

铁摩辛柯是一位力学教育家，他培养了许多研究生，还编写了大量适合于大学力学教学用的优秀教材，计有《材料力学》、《高等材料力学》、《结构力学》、《工程力学》《工程中的振动问题》、《弹性力学》、《板壳理论》、《弹性系统的稳定性》、《高等动力学》《材料力学史》等20多部。这些教材影响很大，被翻译为world各国的多种文字出版，其中大部分有中文译本，有些书至今仍被教学采用。

泊松在弹性理论上的工作

泊松（Simon Denis Poission，1781－1840）出生在巴黎附近的一个贫穷家庭，15岁以前没有受过正规教育。1796年被送到舅父家，之后才参加了数学学习。1789年由于他的成绩为全班**，他被特别准予进入巴黎综合工科学校学习，并且为当时留在该校任教的拉格朗日与拉普拉斯所赏识，1800年毕业任数学教师。

泊松的研究工作的主要特点是利用数学方法去处理复杂的力学与物理问题。他的主要贡献有：在偏微分方程上求解，即位势函数及其在引力场与静电学中的应用问题，他提出概率方法的普遍适用性，并得到了泊松分布律，他在分析力学中引进了泊松括号，在弹性力学中引进了泊松比。

泊松对弹性力学的兴趣是由纳维的原始工作引起的。他在1829年他发表了题为《弹性体平衡和运动》的研究报告，文中也是用分子间相互作用的理论导出弹性体的运动方程，并且发现在弹性介质中可以传播纵波与横波。他还从理论上推演出各向同性弹性杆在纵向拉伸时，横向收缩应变与纵向伸长之比是一个常数，其值为1/4，但这一值与实验有差距。1848年G·维尔泰姆进行实验认为是1/3。泊松引进的这个比例常数后人称为泊松比。

泊松**次得到了板的挠曲方程，其中E为杨氏模量，他取＝0．25。在求解这个方程时他主张附加三个边界条件：剪力、扭矩、弯矩。边界条件的这种提法是不正确的，后来纳维给出了正确的边界条件提法：两个条件，并且给出了边界为简支时的解。他求解了许多具有实际应用价值的圆板的振动问题。

圣维南及其在弹性力学中的贡献

圣维南（Saint－Venant，Adhemar Jean Claude Barre．1797—1886）的父亲是一位颇有名气的农村经济学家，在他的细心教导下，圣维南从小就爱好数学，并表现出突出的才能。圣维南稍长，就到布鲁日公立学校上学，1813年他16岁时通过选拔考试进入巴黎综合工科学校。在该校他表现出卓越的才能，学习成绩名列全班**名。然而一场政治动乱对他的一生产生了巨大影响。1814年反法联盟军队逼近巴黎，学校动员学生为巴黎的防御工事运送武器，圣维南拒绝参加，被学校除名。此后8年，他一直在火药工厂工作。1823年法国政府批准他免试进人桥梁道路学院，两年后他以全班**名的成绩毕业。

1825－1830年，他先后在尼韦奈运河和阿登运河上从事工程设计工作。其间，他利用业余时间研究力学理论。1834年，他向法国科学院提交了两篇关于理论力学和流体力学的论文，并因此在科学界出了名。

1837年，桥梁道路学院请圣维南讲授材料强度理论。当时关于材料力学的ZUI新讲义是圣维南的老师C．纳维（Navier）编写的《力学在结构和机械方面的应用》（1826）该书以纳维在桥梁道路学院讲授应用力学的讲义为基础整理而成。虽然纳维建立了弹性力学的基本方程，但他在讲义中并没涉及它们，仍然采用平面假定求解问题。圣维南则首先试图把弹性理论的ZUI近进展介绍给他的学生，他对固体的分子结构和分子间的作用力的假设进行讨论，并用这一假设解释了应力概念。1864年圣维南对该书修订第三版时，在书中增加了大量的注释，使原书的篇幅增加了九倍。他还讲授了剪应力和剪应变。由此算出主应力。圣维南在教学中提出的一些问题成为他日后进行科研的课题，他的讲义用石印印出，其原稿现在藏于桥梁道路学院的图书馆。

圣维南在桥梁道路学院任教时，还在巴黎市政府兼任一些实际工作。此外，他很早就对水力学及其在农业上的应用感兴趣，并发表过若干篇论文，为此他获得了法国农学会的金质奖章，1850－1852年还在凡尔赛农学院讲授过力学。然而，这些并未影响他在弹性理论方面的研究。1847年他关于扭转的**篇论文发表。1855和1856年他发表的两篇杰出论文系统地阐述了扭转和弯曲问题。1868年以后，圣维南又研究塑性力学，提出塑性流动的基

本假设和基本方程。圣维南一直工作到生命的ZUI后几天，1886年1月2日，他的ZUI后一篇论文发表在法国科学院学报上。1月6日他以88岁高龄去世。

圣维南的研究领域主要集中于固体力学和流体力学，特别是在材料力学和弹性力学方面作出很大贡献。

圣维南**个验证了弯曲基本假设的精确性，所谓基本假设是：梁变形时横截面保持平面；梁的纵向纤维在弯曲时相互之间无应力。

基于对梁的纯弯曲研究，圣维南1855年给出了圣维南原理的ZUI早提法。即：只有当作用于梁两端的外力分布在端截面上的情况与在梁中央各截面上的应力分布情况相同时，所得到的应力分布才与准确解相符。

圣维南提出和发展了求解弹性力学的半逆解法。1853年他关于弹性柱体扭转的报告，法国科学院由A．L．柯西、G．拉梅（Lame）、J．V．彭色列（Poncelet）等组成的委员会给予很高的评价。文中首次提出了半逆解法。由于半逆解法的论文，弹性理论的基本方程才逐步被引人有关材料强度的工程书籍中。

1883年圣维南翻译克莱伯什的德文著作《固体弹性理论》一书出版。他的注释是原篇幅的三倍。其中ZUI重要的是关于杆的振动和碰撞理论。

由于圣维南取得了大量创造性的研究成果，1868年他以力学权威被选为法国科学院院士。他一生重视理论研究成果应用于工程实际，他认为只有理论与实际相结合，才能促进理论研究和工程进步。

周培源的简历

周培源（1902—1993，11，24）出生于江苏宜兴县的一个书香之家。1919年人清华学校的中等科，于1924年毕业于高等科。于同年被选派赴美在芝加哥大学学习，并于 1926年获学土与硕士学位。他是辛亥革命之后我国较早派出的留学生之一。在早期的留学生中学工的占大多数，学理科的是少数，而学理科的又是学实验物理的占多数，像周培源这样学理论物理的，真是凤毛麟角。

周培源1927年在美国加利福尼亚大学攻读，并于1928年获得博士学位。1928年赴德莱比锡大学在海森伯（W．K．Heisenberg）教授领导下工作，1929年转赴瑞士苏黎世高等工业学校在泡利（S．Pauli）领导下从事量子力学的研究。同年回国，年仅27岁的周培源被聘为清华大学物理系的教授。1936年周培源再次赴美，曾参加爱因斯坦领导下的广义相对论讨论班，研究引力论与宇宙论。

周培源数十年从事教学，他培养了数代知名学者与数以千计的物理与力学专门人才。国内早期从事理论物理的人很少，他在清华大学时，理论力学、量子力学、相对论等课门门都不得不由他一人来上，后来这些课逐步交给他的学生去教。国内外物理界与力学界的许多杰出学者如彭桓武、胡宁、王竹溪、钱三强、林家翘、于光远等都曾经受业先生门下。他是当之无愧的一代宗师。

他曾任清华大学与北京大学教务长、北京大学副校长、校长。中国科学院副院长、中国科学技术协会主席、中国物理学会理事长、中国力学学会副理事长。他还是我国ZUI早的国际理论与应用力学联合会的理事。

周培源的科学研究方面，集毕生的精力于两个力学与理论物理的ZUI难的问题：湍流与广义相对论。在两个领域中都取得世人注目的成就。

广义相对论在物理上取得了许多辉煌成就，但从一开始就存在着一个困难，即表达引力场的方程是一个包含10个二阶非线性偏微分方程的方程组，10个方程之间又有4个独立的非线性偏微分的恒等式（Bianchi恒等式），就是说只用引力方程得不到10个引力函数的确定解。周培源主张另外引进物理条件求解，在20、30年代他用这种办法得到了轴对称静态引力场的若干解。70年代他与他的学生们把严格的谐和条件作为一类物理条件从而得到了一系列的新的解。周培源在广义相对论方面在国际上是以“坐标有关论”而独树一帜。

在湍流领域，他ZUI早（1940年）从雷诺方程导出了二阶与三阶关联函数所满足的动力学方程组。后来他又于 1945年提出了两种求解这组方程的办法。他的这些工作被国际上誉为“湍流模式理论的基础”。50年代以后，他与学生们解决了湍流衰变期的二元与三元关联函数。70年代他又提出了湍流中“准相似”的概念。这些工作后来都得到实验证实。

在“文化大革命”的那场浩劫中，当“理科无用论”盛行时，周培源是知识分子中敢于顶这股邪风的中流服柱。1972年周培源先在高教部理科座谈会上发言，后在《人民日报》上发表了《对综合大学理科教育革命的一些看法》，又直接上书周恩来陈述应当重视基础理论的主张，并且提出关于如何加强基础理论研究的建议。例如他列举牛顿力学当年并不是为了直接解决生产问题而是解决行星的运行问题的，他还举早先发展核物理的理论研究后来才有核工程的出现，用来说明理论研究的重要性。他的这些中肯意见却受到了批判，批判他的人把他的论点歪曲为科学研究的选题要考虑“三百年后用得上”，然后在国内性的刊物上大加讨伐。周培源没有被批倒，他那刚直不阿的形象深深留在知识分子心中。

如果说科学精神就是执着地追求真理、坚持真理解卫真理，那么周培源教授的一生就是这种执着精神的写照。他在晚年曾经这样来总结自己的一生：“独立思考、实事求是、楔而不舍、以勤补拙。”

钱学森的简介

钱学森（1901）出生于上海，自幼随父在北京接受初等与中等教育。1929年中学毕业后他考人上海交通大学。1934年在交通大学毕业后，考取了清华大学的公费留学。1935年赴美在麻省理工学院航空系学习，1936年转学到加州理工学院师从冯·卡门学习力学。1939年6月钱学森以《高速空气动力学》为题的论文获得博士学位。后来成为冯·卡门的助手留校工作。1942年美国军方委托加州理工大学举办喷气技术训练班，钱学森是教员之一，与美国陆海空军人员有了接触，后来美国从事火箭导弹工作的军官中有不少是他的学生。1945年在冯·卡门的推荐下，钱学森被美国空军聘为科学咨询团成员。同年5月二次world大战结束前，钱学森随团去欧洲考察英、德、法的火箭技术发展。这时他被定为副教授。

1946年钱学森转到麻省理工学院，次年升为教授。1948年后，钱学森加紧了回国的准备，其间他曾受到美国当局的怀疑与迫害。经过不断努力，又经过中华人民共和国的外交交涉，钱学森终于在1955年回国。

钱学森回国后历任中国科学院力学研究所所长、中国力学学会**届理事会理事长、1958年任中国科技大学近代力学系系主任、1965年任第七机械工业部副部长、1970年任国防科学技术委员会副主任、中国科学技术协会主席等职。

钱学森是杰出的力学家、航空专家与火箭专家。作为力学家，他在流体力学、固体力学、一般力学方面都有重要贡献。作为航空与航天专家，他在空气动力学，飞机火箭有关的结构力学、飞行控制方面都是造诣很深的专家。他是一位有多方面才能的学者。他是中国研制火箭、导弹与航天事业的开拓者。

1956年10月，在聂荣臻元帅主持下经过钱学森组建的、以研制导弹为重任的国防部第五研究院宣告成立，钱学森为分配来的156名大学毕业生开始了《导弹概论》的培训课。后来这批学员成了中国研制火箭、导弹的骨干力量。1960年成功发射了近程导弹，1964年发射成功了中近程导弹，1966年中近程导弹与原子弹的联合发射成功，1970年4月24日中国的**颗人造卫星成功发射，这些无一不包含着钱学森的学识、智慧与辛勤劳动。

在力学的科学研究方面，由于钱学森的涉猎很广，要想在短短的篇幅中全面介绍是不可能的。

在科学技术上，超前的眼光是科学家ZUI可宝贵的素质，纵观钱学森一生所涉猎过的研究选题，人们可以有一个深刻的印象。在飞机还在低速飞行时，从30年代起，他选择考虑空气的可压缩性、跨声速、超音速空气动力学课题并且得到了像被称为卡门一钱方法等那样的重要成果。当人们大多在探讨弹性结构的线性理论时，他却从事薄壳的非线性稳定性理论的研究，取得了这方面的开创性的成果。他参加了火箭技术的早期探索研究。他ZUI早用指导

控制与制导的一般眼光，并且探求它的普遍原理与方法，写出了《工程控制论》于1954年出版。此外他还提出应当重视物理力学、系统科学研究的有益见解。

由于钱学森的科学技术贡献，1991年10月16日国务院、中央军委授予他“国家杰出贡献科学家”的荣誉称号。

伯努利定律

丹尼尔·伯努利（Daniel Bernaulli，1700－1782）是约翰·伯努利的儿子。伯努利家族中连续几代都有杰出的数学家或力学家，这个家族原来居住在荷兰，后来因为信仰新教而被逐出荷兰。1705年全家回到瑞土。他的哥哥也是一位数学家。

丹尼尔在1738年出版的《流体动力学》中，将力学中的活力守恒原理引入流体力学，给了一个系统的阐述。

丹尼尔认为：“我的理论是新的，因为它既讨论压力也讨论流体运动。”即在他的理论中，既讨论平衡也讨论运动。

丹尼尔·伯努利研究的ZUI重要的结果现今称为伯努利定理。他利用一个充满流体的容器，下部开一小孔，讨论其活力守恒，ZUI后得到随着流体的速度增加，其压力减小的结论，也就是

式中为孔口流速，为液面距孔口的高度，为重力加速度。

从这个公式，可以得到托里拆利定理，即

马赫在气体力学上的工作

马赫（Ernst Mach,1838—1916）是奥地利的力学家、物理雪家、心理学家、哲学家。早年在维也纳大学就读，1860年在那里获得博士学位。1866年任该校教授，以后到布拉格大学任教，于1895年又回到维也纳。

1881年，马赫在巴黎国际展览会上，听到了一个比利时的炮师的报告。这个报告讨论了从炮口喷出的压缩空气的破坏作用，并且认为炮弹携带的压缩空气超前于炮弹又引起像爆炸一样的机械破坏效应。这个问题引起了马赫的兴趣，1885年他发表了一篇文章公布了1884年拍摄的4种不同波（飞弹波、声波、火花波、抛体激波）的照片，在这篇文章中，他引进了流速与声速之比的参量，这就是后人称为的马赫数。马赫早期曾用纹影技术研究抛射体的飞行，他1887年写的几篇文章解决了：以声速传播的球面波问题，引进了马赫波的概念。他的结论是：锥面母线与物体方向所成的角度与，的关系是，这个数就是马赫数。马赫是ZUI早系统得研究力学史的学者，他的《力学史评》是对到他那时为止的力学史的总结。其中的一些论述对牛顿的一概时空观念给以批评，对后来发展相对论力学具有启迪作用。

拉格朗日生平

拉格朗日（Joseph Louis Lagrange，1736－1813）是数学和力学史上的一位重要人物。他的一生可分为三个时期，即早期在意大利的都灵（1736－1766）,中期在普鲁士的柏林（1766－1787），后期在法国的巴黎（1787 —1813）。

都灵是他的出生地，他很早就锋芒毕露。他在18岁时开始写论文。在都灵ZUI重要的事件是他1755年致信欧拉参加关于变分原理的讨论，给出了求泛函极值的分析方法。此工作为欧拉所赏识，使他一举成名。据说他19岁时（一说是16岁时）被聘为都灵皇家炮兵学院的数学教授。这位还带几分孩子气的教授上课时，听课的学生都比他年龄大。

拉格朗日在21岁时，以他为首的一批青年组成了都灵科学协会，并创办了一本杂志(1759年出版),杂志的前三卷大部分登的是拉格朗日的论文。大约从19岁开始，当他介入变分法的讨论时他便开始了《分析力学》的构思。拉格朗日有一度写信给达朗贝尔，表示要放弃数学。达朗贝尔复信劝告他说：“看在上帝的面上，不要放弃工作。工作对于你是一切消遣中ZUI有效的消遣。再见吧，也许这是ZUI后一次了，多少记住这个在world上ZUI爱护你、ZUI尊敬你的人吧。”

1766年，欧拉应聘彼得堡科学院而要离开柏林普鲁士科学院，他举荐拉格朗日接替自己。从此拉格朗日成为该院数学部主任。这一段是他一生创作的鼎盛期。他在三体问题、行星运动、流体力学、微分方程、数论、概率论等方面都作出了重要贡献。

1787年，他来到巴黎科学院，他在这里出版了《分析力学》，并且参加了法国大革命后科学院成立的度量衡委员会的工作。

拉格朗日曾结过两次婚，没有于女。

1813年4月10日，拉格朗日去世了，他在弥留之际所说的ZUI后的话是：“我过完了我的一生，我在数学中得到了一些名声。我从不恨任何人，我没有作过什么坏事，死会是很好的；但是我的妻子不希望我死”他就这样坦然地离开人世。拿破仑称赞他是“数学学科高耸的金字塔”。他去世后近二百年来，现代科学技术的发展愈来愈证明他开拓的分析力学的重要，无论从数学上还是从力学上它仍然是人们进入现代科学必要掌握的篇章。

拉格朗日在他19岁时便开始构筑《分析力学》的框架，直到1782年他写给法国数学家拉普拉斯的信中才宣告《分析力学》完稿，其间经过了长达30多年的历程。当时刚刚从政，在法国当了大官的大数学家拉普拉斯帮助安排在法国出版这本书，大数学家勒让得（Legendre）担任了这本书的编辑。到1788年正式出版。之后拉格朗日对这本书又作了补充和修改，在1816年，拉格朗日去世后三年第二版出版了。

这本书的第二版共分为两卷，有785页之多。**卷的一半是静力学，主要讨论质点组和流体的平衡问题，**卷的后一半和第二卷是讨论动力学的，动力学共分13章。

达朗贝尔

达朗贝尔（Jean le Rond d’Alembert,1717—1783 ）是法国人，他是在教堂台阶上的一个弃婴。Jean le Rond 就是教堂的名字，养育他的父母姓d’Alembert。他在成年后，便离开了他的养母。他的养母派人找到了他，他说：“你是我的后母，装玻璃工人的妻子才是我的真正母亲。”他是一位哲学家、数学家、天文学家、力学家。他还是当时法国百科全书派的主将。