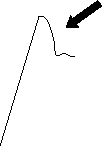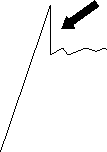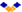(実験テキストから抜粋、一部、説明時の文章も加筆している)
|
1.目的
金属材料( SS-400材)を用いて,引張試験を行うことによつて,引張試験の方法を習得し,応力ーひずみ曲線,材料の機械的性質を理解することを目的とする。
2.原理
引張試験は,材料の強度を測定する最も基本的な試験である。試験は,材料に一定の伸びを試験片に与えたとき,どの程度の大きさの抵抗力を示すかを連続的に伸びを与えて調べるものである。
* 引張試験機
試験機は油圧によって試験片に伸びを与えるものと電動モーターによって与えるものに大別できる。油圧式は大荷重の容量(数千トン)のものまであり,建築,土木材料の性能試験,実物大の部材,部品試験に使用される。通常の鋼材検査証明書等の機械的性質はこの試験機を使用して求める。
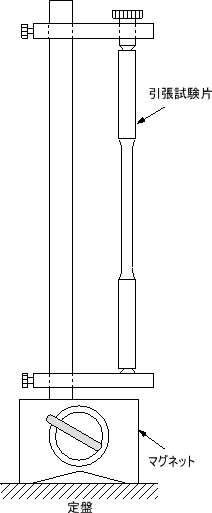
本実験では,後者のネジ式引張試験機(インストロン社が最初に製造したことからインストロンタイプとも言う。)を用いる。図1は試験機のシステムを示したものである。クロスヘッド上部に荷重検出器(ロード・セル)を固定し,さらにこれに試験片掴み具(チャック)を連結し試験片の上部を固定する。一方,試験片の下部は掴み具で掴み,これを剛体枠下部に固定する。クロスヘッドは,モーターで、両側のフレームにあるネジ棹(さお)を回転させることによって上下し,試験片は一定の速度で引き伸ばされる。この試験機の特徴は一定の変位速度で負荷することができ,変位速度の設定範囲が大きい(0.005 ~500 mm/min)ので,強度の低い材料から高い材料の試験をすることができる(伸びが小さくとも精度良く負荷できる)。試験機の容量(試験で負荷できる最大荷重、約30トン以下)は油圧式ほど大きくない。材料の強さは、変位速度の影響を受けるが、ネジ式引張試験機は、荷重が変化しても常に一定速度で伸びを負荷できるので変位速度の影響を考えなくとも良い。
ある量の伸びを試験片に与えるのに必要な荷重(材料の抵抗力)は,ひずみゲージ式ロード・セルによって電気信号に変換される。一方,伸びは試験片に直接取り付けられた変位計ないしクロスヘッドの移動量をネジ棹の回転量をロータリーエンコーダなどで電気信号に変換する。そして,これらの電気信号をX-Y記録計を用い,荷重信号をY軸に,伸びの信号をX軸に入力することによって,連続的に荷重-伸び関係曲線を記録することができる。本試験機の場合は,記録紙が設定した倍率で試験片の伸びに比例して送られるようになっている。
荷重-伸び関係曲線から応力-ひずみ曲線,設計の基礎となる種々の機械的性質が得られ,材料の引張に対する力学的特性が理解できる。
3.実験装置,器具
容量10トンネジ式引張試験機,マイクロメータ,ディジタルハイトゲージ,定盤等.
4.実験方法
4-1. 試験前の準備,測定
本実験で使用する材料はSS-400(SSはStructure Steel、構造用鋼の略,引張強さ400 MPa以上,旧JIS SS-41,引張強さ41kgf/mm2 以上)で,試験片の形状,寸法を図2に示す。
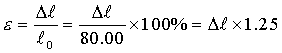 (a) 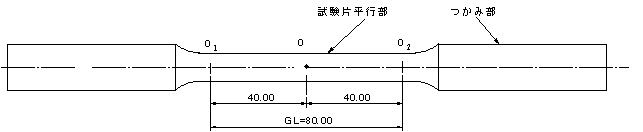 (b)
図2 引張試験片の形状,寸法
(1).試験片直径doの測定
O1近傍の直径をマイクロメータで2方向から測定する。O,O2についても同様に測定し,計6つのデータの平均値をDoとする。O1, O2の測定の際はアールの部分にかからないように注意のこと。 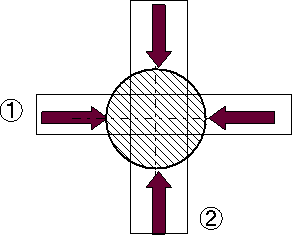 直径の測定は二方向から マイクロメータの原理と測定方法はこちら ノギスの使い方はこちら (2).標点のけがき
平行部の一部に(けがき線を引く近傍)けがき用塗料を塗り,試験片取り付け装置に垂直に固定し、平行部の中心位置Oをディジタルハイトゲージによって求め,この位置から上下(40)mmの位置O1,O2 にけがき線をけがく。従って,標線間距離(GL, Gage Length, 標点間距離とも言う)O1O2はGL=Lo=(80.00)mm である。このGLがひずみを計算する場合の変形前の元の長さになり、この長さがΔLの伸びを生ずるとしてひずみの計算をする。
4-2.引張試験
引張試験は,下記の要領で行うが試験機の操作は取扱説明書を予め良く読み,指示に従いながら慎重に行うこと。
(1).試験条件の設定(図1で示した試験機の場合の設定値)
・試験機荷重レンジフルスケール ( 10 ) tonf
・負荷速度 ( 10 ) mm/min
・記録計Y軸のフルスケール ( 10000 ) kgf
・記録計X軸の記録紙送り倍率 伸びの( 10 ) 倍
*赤文字は学生が説明を聞いてテキストに記入。最初は空白になっている。 (2).試験中観察すべきこと
・降伏現象,試験片表面の反射の変化,くびれの開始時期と荷重-伸び曲線との関係
4-3.破断後の測定,観察 破断切口をしっかり突合せ,試験片固定治具に垂直にセットし、以下の順序で計測を行う。
(1).破断後の標線間距離O1O2をデジタル・ハイトゲージにて5回測定し,これらの平均値をLfとする。
(2).破断部最小直径をナイフエッジ付きマイクロメーターで種々の方向から6回測定し,平均値をdfとする。
(3).破断面を観察し,破面の特徴をとらえてスケッチする。
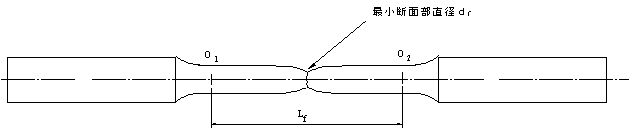 図3 破断後の試験片,最小断面部の直径とO1O2の長さの測定
5.結果の整理
測定結果はテキストの表を利用し,整理する。特に,有効数字の扱いには注意すること。Appendixに有効数字の簡便的扱いの例を示した。四捨五入した場合は四捨五入する前の値を必ず記すこと(例 OOOO ≒ OOO mm)。
5-1.変形前の直径do ,標点間距離(Gage Length)Lo,破断後の最小断面部直径df,破断後の標点間距 離Lfの測定(結果は表1,2に記入)
表1 do ,Loの測定データ表
*平均値の有効数字に注意!!
平均値は測定値より有効数字が少なくなることはない
表2 破断後の破断部最小直径df ,破断後の標点間距離Lfの測定データ表
5-2. 応力-ひずみ曲線の作成 表3に記入
(1).記録紙から伸び,荷重データを読む
記録紙上の荷重-伸び曲線データから,横軸の伸び(ΔL)に対する荷重Pの値を読む。一般に,変化が急激な部分は細かく読み,変化が緩やかな部分は間隔を開けて読む。伸びは記録紙X軸倍率10のとき,実際の伸びは10倍に拡大されて記録される。すなわち、記録紙10mmが、試験片の伸び1mmに相当する。本試験機の場合,記録紙X軸の目盛りは10 mm 間隔になっているので伸びに対する荷重を読んだ方がよい。変化が急激な箇所は記録紙10mm間隔、D点付近は20から30mm間隔程度。ただし、A,B,C,D,E点(図5)の伸びと荷重は必ず読む。B点は、上降伏後からC点の間で一番荷重が低いところ。 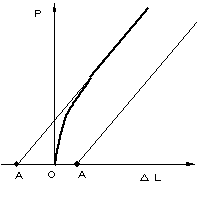 図4 データの補正 (2).記録データの補正
記録計から得られるデータは試験スタート時、図4のようになる場合が多い。フックの法則に従い、荷重と伸びの関係が直線になるべきところ、0点付近は直線にならない。これには,種々の原因がある。図の場合に,最初,伸びが余り生じていないが荷重は増加している。実際には,試験片は伸びているのであるがなんらかの原因で記録紙に記録されない。これを補正する必要がある。直線部分(フックの法則が成り立つところ)を延長し,横軸との交点をAとする。AOの伸びが補正すべき伸びで,この場合はこの値をすべての伸びΔL’に加える。AがO点より右側にあるときΔL’からAOの伸びを差し引く。この処理を行なった伸びをΔLの欄に記入する。
*メカの部分は必ずクリアランスを有している。歯車,ネジ部などである。これ等が影響して,記録計に記録される量と実際の物理量と異なってくる。 (3).次に,記録紙から読んだ荷重P,伸びΔLから,応力σとひずみeを計算する。
公称応力σはすべての荷重Pを変形前の断面積Aoで割って求められる。
σ = P/Ao ( MPa) --------------------- (1)
ただし,Ao= πdo2/4,do [mm],P[N], 1 kgf=9.8 N, 1 N/mm2=1 MPa
公称ひずみeは伸びΔLを標点間距離Loで割って求められる。
e = ΔL/Lo (mm/mm or e×100 %) ------- (2)
(4).応力ーひずみ曲線の作成
セクション・ペーパーを用いて,縦軸に応力σ[MPa],横軸にひずみe[%]をとり,データをプロットする。曲線の部分は自在定規または雲型定規などを用いて滑らかに引くこと。
(5).上降伏応力,下降伏応力,引張強さ,伸び,絞り値の計算。
(a).上降伏応力(Upper Yield Stress ),σuy
σuy = Puy / Ao = 4Puy/(πdo2) MPa
(b).下降伏応力(Lower Yield Stress ),σly
σly = Ply / Ao = 4Ply/(πdo2) MPa
(c). 引張強さ (Tensile Strength ),極限引張強さ(Ultimate Tensile Strength),U.T.S
σu = Pu / Ao = 4Pu/(πdo2) MPa
(d). 伸び (Elongation ) , φ
φ = 100 ×( Lf - Lo)/Lo %
(e). 絞り,断面縮小率,ψ,R.A(Reduction of Area)
ψ = 100 × (Ao- Af)/Ao %
ただし、Ao=πdo2/4,Af=πdf2/4
*Pは、tonfで与えられているので(1)式に示す単位換算が必要である。
 図5 炭素鋼の荷重ー伸び曲線 表4 SS-400 材の機械的性質
6.考察
本来,考察は実験で得られた結果が従来の研究結果から推察して,理論的にも現象的にも説明がつき,妥当なものであるか検討することによって,従来の研究結果より一歩進んだ知見を得ることにある。工学実験では,実験で得られた結果や現象が講義において学習した知識で説明できるか,あるいは理解できるかを調べることが考察である。感想と考察とは異なるので注意すること。
幸いなことに,本実験は,材料力学,材料科学ですでに勉強したことの実践であるので理解しやすい。教科書(はじめての材料力学)を利用して次の問題を解くことで考察すること。
(1).実験で得られた結果(降伏応力,引張強さ,伸び、絞り)とSS400の規格の値を比較せよ。
(2).破断面をスケッチし,特徴ある部分の名称を記入せよ。
(3).降伏点が明瞭に表れない場合の材料の降伏応力(耐力)を求める方法を図を用いて述べよ。
(4).最大荷重点の現象について調べよ。
(5).応力ーひずみ曲線において,リューダース帯とはどの部分を言うのか.このとき,試験片ではどのような現象が生じているか。
(6).ひずみ硬化の現象を転位論を用いて説明せよ。
7.報告書の作成について
・テキストをそのまま写しても意味がないので,1~4は自分で要約して文章を書くこと。
・結果は有効数字に注意してテキストに示されている形式に合わせて整理すること。
・表1~4のデータ,応力ーひずみ曲線は報告書に添付すること。
・機械的性質の各値を求める数値計算式は記すこと。
【計算例】
↑ 数字を丸める前の値は必ず書くこと 引張試験 Appendix
1.測定値の取扱い
測定値の取扱いで大切なことは,計算では(特に電卓)大きな桁数になっても,実際に数値として意味のあるデータとするためには何桁までの数値を取るかと言うことである。
(1).有効数字と計算
3.249と言う数字は純数学的には 3.249000・・・・・という意味であるが,測定値の場合は,末尾の数値が四捨五入されて 9 になったと言う意味で,測定値Mは次の範囲にある。 3.2485 ≦ M < 3.2495
このようなことから一般には,測定値は末尾の数値までが意味があり,それ以下の桁については不明である。このように意味のある数字を『有効数字』という。また,測定値においては,例えば目盛りを有するもので測定する場合,目分量では最小目盛りの1/10まで読むことができるのであるから,最後の桁の数字は目分量で読んだことを意味する。従って,そのひとつ前の桁は最小目盛りの位置を表すことになる。
【例】 1. L= 12.3 mm 有効数字 3桁
2. L= 12.300 mm 〃 5桁
3. L= 0.0034 mm 〃 2桁
4. L= 1200 mm 〃 4桁
5. L= 2.34 ×104 mm 〃 3桁
例3のように,小数点以下の桁数を表す0は有効数字には数えないが,例4のような場合の0は有効数字に数える。例4で有効数字が2桁である場合は,例5のような表現を用いて,1.2×103 mm のように書くべきである。
また,例1と例2を比較すると,数学的には同じ値であるが,測定値の場合は意味が異なる。例1の「3」は目分量で読んだ結果であり,「2」は,最小目盛りの位置を表すので,1 mm の最小目盛りを有する測定器(例えば物差し)で読んだことになる。例2では,最後の「0」は目分量の読みの結果ちょうど「0」であり,その前の「0」は最小目盛りの位置を示し,1/100 mmの最小目盛りを有する測定器(例えば,マイクロメータ)を用いたことを示している。
(2).測定値どうしの計算
有効数字の異なる2つ以上の測定値を用い,計算してある量を得るときの有効数字の扱い方である。
・加減の計算
小数点以下の有効数字の桁数を揃えるようにする。小数点以下の有効数字の桁数の最小のものより一つだけ多くとって計算し,最終結果は測定値の中で小数点以下の有効数字の桁数の最小のものに揃える。 【計算例】
16.5 mm 16.5 mm
+ 8.1421 mm =======> + 8.14 mm
24.6421 mm 24.64 mm
無意味になるので右のように計算する。
最終結果は ---------------------- 24.64 ≒ 24.6 mm
さらに計算を続けるときはこの値24.64を使う 有効数字3桁(16.5による) ・測定値どうしの剰余計算
測定値の中で,有効数字の最小のものに着目し,このものより一つ多い桁に揃えて計算し,最終結果は有効数字の最小のものに合わせる。
【計算例】
0.078 × 26.8 × 1.028 = 2.1384792
↑ ↑ ↑ ↑ 無意味になる*
有効数字2桁 3桁 4桁
*無意味になる根拠 仮に,0.078の測定値で、測定できなかった有効数字3桁目を0.0789として計算してみると, となり,結果の3桁目の値が変わり,測定できなかった値が結果の3桁目に影響していることがわかる。 次のように計算する。
最小有効数字2桁 3桁 3桁:最小有効数字より1桁多く取って計算
↓ ↓ ↓
0.078 × 26.8 × 1.03 = 2.153
最終結果は --------- 2.153 ≒ 2.2
↑最小有効数字2桁(0.078)
この方法は,便宜的な方法であり,利害関係が生ずる場合は,JISで定められた「数字の丸め方」に従うことになる。例えば、寸法の有効数字を1桁多く要求されると、精度を上げる必要があり、工作精度が必要となりコストがアップするので、発注者と製造者の間で利害関係が生ずる。 2.荷重計(ロードセル)
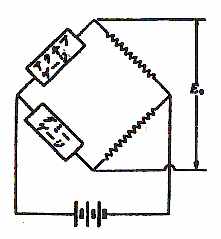
ロードセルの構造は図のようになっている。丸棒に抵抗線ひずみゲージが接着剤で貼り付けてある。荷重と直角方向のダミーゲージは温度変化による抵抗値の変化を打ち消すためにある。
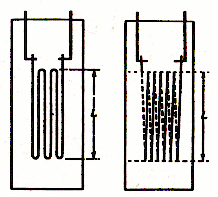
ひずみゲージは直径 0.025 mm 程度の細線を図のようにグリッドやソレノイド状に曲げて接着剤で薄紙に貼り付けたもので,Lは 1.5 ~ 200 mm 程度,25 mm のものが一般的で抵抗値は 50 ~2,000 Ωであるが,120 Ω,350 Ω のものがよく使用される。
電気抵抗Rは細線の断面積A,長さL,比抵抗ρのとき,R = ρL / A で表される。貼り付けた材料が荷重を受けて長さがΔLだけ変形すると貼られたひずみゲージは材料と共に引き伸ばされるので抵抗値はΔRだけ変化する。 ΔR/R=k・ΔL/L
この抵抗値の変化をホイーストン・ブリッジ回路で検出し増幅すると材料のひずみe=ΔL/Lが分かり,材料のヤング係数,断面積から作用している荷重Pの大きさが測定できることになる。
P=σ・Ao=(E・e)Ao=E・(ΔL/L)・Ao
ひずみゲージは変位センサーであり微小な変位,ひずみの測定に用いられ,これらを応用して,重量,力や圧力も測定することができる。
表3 応力ーひずみ曲線作成データ
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ここまでは、以前担当していた3年生の工学実験「引張試験」のテキスト原稿から抜粋したものです。 測定結果の処理の一例 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
いずれも異なる位置で測定 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ■数値の計算 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 記録紙からの伸びの補正 ④= ΔL=③+0.2= ΔL'+0.2 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
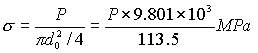 ② = ①×9.801×103/113.5 MPa ② = ①×9.801×103/113.5 MPatonf→ kgf → N |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
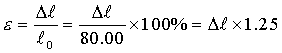 ⑤ = ④×1.25 % ⑤ = ④×1.25 % |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| *②は有効数字4桁で充分 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Ao=πdo2/4=3.142×(12.021)2/4=113.51 mm2=1.135×102 mm2 *πの値は,荷重の有効数字より1つ余計に取り,π=3.142を使う。 *「はじめての材料力学」の教科書で推奨しているように、計算の際、文字式に代入するとき、荷重[N]、長さ[mm]など単位を確認するとともに、○.○○○×10o の形にする。 仮数部と指数部を別々に計算すると電卓の打ち間違いが少なくなり、暗算でもおおよその値が確認できる。次の上降伏応力σuyの計算式を見ると、仮数部は、おおよそ、60から70の間、指数部は10となるので、600~700の間の値と結果が予想できる。 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ■上降伏応力σuyは,Puy=6.01 tonf = 7.01×9.801×103 Nであるから, |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
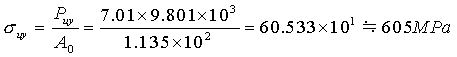 測定値は,Puy=7.01 と do=12.021で,最小有効数字は3桁。重力加速度などは最小有効数字より1桁多く取って,g=9.801を用いる。最終結果は,最小有効数字は3桁に合わせて,4桁目を四捨五入して,3桁「605MPa」とする。 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ■下降伏応力σlyは,Ply=Pb = 5.76 tonf = 5.76××9.801×103 Nであるから, | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 有効数字は上降伏応力と同様である。 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ■引張強さσuは Pu =8.46 tonf = 8.46×9.801×103 Nであるから, | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 有効数字は上降伏応力と同様である。 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ■伸びeは | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
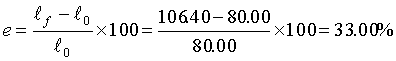 有効数字は 5桁と4桁であるから,結果は4桁とする。%の100は測定値ではないので注意のこと。 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
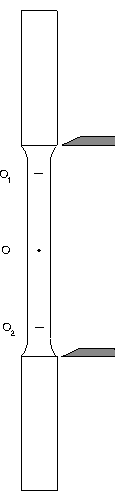 有効数字は5桁と4桁であるので結果は4桁とする。 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
SS400 の機械的性質
*最終結果は有効数字に注意して記載する。 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
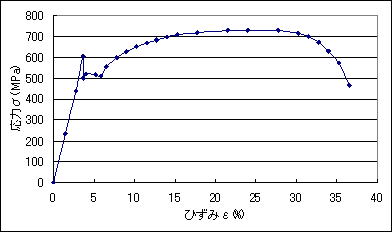 付図7 応力ーひずみ曲線 Excelで描画 最初の列にひずみ、次の列に応力を取り、[データ範囲選択]→[グラフ]→[散布図]→[平滑線とマーカ]を選択 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
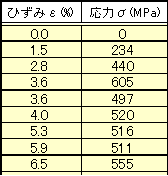 黄色のデータ範囲選択 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
考察の要点
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ■考察して欲しいその他の事項 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 付図8 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| *実験で使用したSS400はミルシート付きの材料であったが、一般のSS400と比較して、σu=731MPaであり、かなり強度の高い材料であることが分かる。実用材の特徴を理解する上ではSS400の性質を知ることは必要であるが、作り方がラフな場合もあり、研究用としては余り使用しない。特に建築用の鉄筋は再生鋼が多い。研究室では石油タンクの腐食の研究を行っていたので、タンクの材料であるSS400の疲労や腐食の研究に用いていた。このときは、必ずミルシート付きのSS400を用いている。 *この実験例では、上降伏後、急激に荷重は低下しているが、試験片取り付け方で変わってくる。じわじわ締め付けると降伏が明確に表れない場合が多い。試験片を取り付けるときは、一気に締め、衝撃荷重を与えると良く固定される。 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
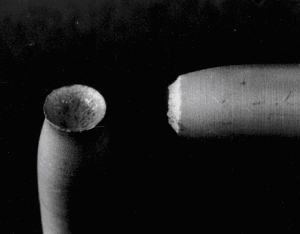 SS400のカップアンドコーンの破断面(付図7の実験例のものではありません) このようにきれいなカップ状に破断することはまれです。一部分欠ける場合が多い。 この破面の電子顕微鏡写真など |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ■引張試験では材料の重要な機械的性質(力が加わったときに示す性質)が得られる |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 機械の部品や構造物の部材が荷重に長期間耐え,その形を保って,壊れることなく安全にその機能を発揮するためには適切な材料とそれらの形状と寸法を与える必要があります。そのために、材料力学では使用する材料の強さを考慮したうえで,作用する力と部品や部材の形状・寸法との関係を明らかにします。材料力学では,材料の強さとして,変形が大きいと機械の精度などが保たれない場合は下降伏応力σlyを,多少変形が許される場合は引張強さσuを材料の強さとして採用します。しかし、いずれの場合も安全係数を取り入れ、余裕を持って設計しますので、塑性変形のような大きな変形をすることはありません。伸びと絞りは変形の度合いを表します。これらの値が大きいほど大きく変形してから破断し、銅やアルミのような延性のある材料になり、小さい程、鋳鉄などのもろい材料です。塑性加工などするときどれくらいまで変形させることが出来るかの目安となります。また、材料が低温環境や衝撃荷重などの条件下で使用されるとき、ぜい性破壊が生じます。このとき設計段階では使用材料の伸びと絞りを参照し、大きな値の材料を使用します。このように、実験室での引張試験で重要な材料の機械的性質が得られます。 材料としては強度が高く、粘さ、靱性がある(伸びと絞りが大きい)のが理想ですが、実際は、強度(引張強さ)が高いと硬くもろく、伸びと絞りは小さく、伸びと絞りが高いと強度が低いのが一般的です。合金により、強度と粘さの相反する性質を両立させるかが合金の目的の一つになっています。0.8%の炭素を含む共析鋼は、柔らかいフェライトと鉄と炭素の化合物で硬いセメンタイトが層状になっている組織(パーライト組織)からなり、複合材料のようになっている。強さと粘さを有し、工具鋼などに使われています。 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
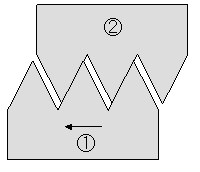
| ■クリアランスについて ----- 0点の補正 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
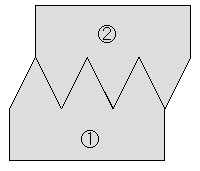
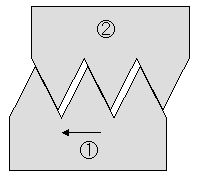
| 下の図で、①のネジを回転させ②を移動させる場合、図Aのようにクリアランス(隙間)が全くない場合、摩擦の問題、工作精度の問題などが生ずる。一般にネジや歯車などの噛み合わせは図Bのようにクリアランスを設けている。図Bの状態から、①を回転させ矢印の方向に移動させた場合、図Cのようになって初めて②は移動する。すなわち、①の移動量に対し、クリアランスの量が②の移動量に反映されないことになる。一端接触すればその後は方向を変えなければクリアランスは問題ない。 図DにおいてA点が0点の左側の場合は、荷重は作用しているが伸びが生じないことを示している。記録紙は歯車を介して伸びに比例して送られる構造になっており、歯車が使用されている。このクリアランスの影響が出ている。A点が0点の右側の場合は、伸びが生じているが荷重は作用していない場合で、試験片つかみ部のクリアランスや試験片に接触する部分(フェイス)が試験片に食い込むなどの影響の可能性がある。今までの経験ではA点が0点の右側の場合は非常に少ない。試験片の固定の仕方が甘い時に生ずる。 ハイトゲージなどのネジを使った器具で測定したり、ケガク場合もこのクリアランスを考慮して、常に同じ方向にネジやダイヤルを回して合わせる必要がある。 伸びが小さい範囲では、このような問題も含まれるので、応力ーひずみ曲線からヤング係数を求めるのは誤差が入ることが考えられる。ヤング係数は物理実験のように曲げ変形から求めた方が精度がよい。 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 図D |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ■応力-ひずみ曲線の形状 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| いろいろな材料関係の教科書や書籍で示されている低炭素鋼の応力-ひずみ曲線の上降伏点近傍の形状を見てみると、次の3タイプに分類される。 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| おそらく、油圧式で実験を行った方は(a),(b)のように描くと思われる。私は大学院時代からネジ式を使っているので(c)のように描く。ネジ式の場合は、上降伏点から荷重が瞬時に垂直に下がる。 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ■ケガキ線 試験片取り付け装置(自作)に引張試験片を垂直に固定する。下部の試験片肩部にハイトゲージの刃先を合わせ、0点を取り、上部試験片肩部に刃先を合わせて目盛りを読み、この目盛りの1/2の位置が平行部の中心位置O点となる。この位置にハイトゲージを合わせ、再度0点を取る。この位置からディジタルハイトゲージで上下(40)mmの位置O1,O2 にけがき線をけがく。結果的に、標線間距離(GL, Gage Length, 標点間距離とも言う)O1O2はGL=Lo=(80.00)mm となる。 クリアランスのところで説明のように、ハイトゲージを合わせるときは、一方向から合わせる。下から上に移動させて目的の数値に合わせる。超過した場合は、もう一度刃先を下げてから上に移動させて合わせる。 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
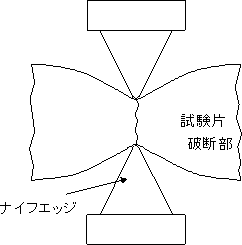
| ■ | 破断部最小直径の測定は、通常のマイクロメータでは出来ないので、アンビル(anvil)とスピンドル(spindle)に図のようなナイフエッジの付いたマイクロメーターで測定する。 |
 |
|
| SS400のJIS規格の一部 ■化学成分 ●SS400 P 0.050%以下 S 0.050%以下 備考: 必要に応じて、 P, S 以外の合金元素を添加してもよい。 *炭素量は指定されていない ■機械的性質(14A号試験片) ●降伏点又は耐力 245MPa 以上 ●引張強さ400 ~510MPa ●伸び22%以上 |